The null evolutionary model
In 1908, G. H. Hardy (a British mathematician) and Wilhelm Weinberg (a German doctor) independently formulated a hypothetical model, showing how - under specific circumstances - the genetic composition of a population would not change. This analysis of Mendel's First Law resolved a divergence of opinions (and outright misunderstandings), regarding its expected outcome. Dissolving this riddle - ultimately - led to the acceptance of evolution as a shift of an allele frequency in a population over time.
The "Hardy-Weinberg equilibrium" theorem states that evolution will not take place - if certain conditions obtain. It demonstrates how allele and genotype frequencies remain stable (in a state of equilibrium) - when undisturbed by intervening "forces of nature", and it paints a picture of an idealized, null-evolutionary scenario.
- Mendel's First Law
-
1. A gene can exist in more than one form.
2. Individual organisms inherit two alleles for each trait.
3. When gametes are produced by meiosis, allele pairs separate leaving each cell with a single allele for each trait.
4. After combining when the two alleles of a pair are different, one is dominant and the other is recessive.
For one trait, an individual carries two, unblending versions of a gene. During meiosis (gamete formation), the two versions of the gene pair separate from each other to form gametes. When gametes unite at fertilization, they combine at random.
- Dominant
- an allele (X) which produces the same phenotype whether it is heterozygous or homozygous
- Recessive
- an allele (x) that is expressed only when homozygous; the recessive allele is not expressed in the heterozygote phenotype
Any population - which exists in Hardy-Weinberg equilibrium, the ratio of homozygous dominant (XX) to heterozygous (Xx) to homozygous recessive (xx) is exactly 1:2:1.
Mendel's first law permits the following outcome: In a large (theoretically infinite in size) sexually reproducing population, allele and genotype frequencies will remain constant across generations - unless disrupted by evolutionary processes acting on them; that is, no evolution will occur - if the following conditions (1-7) hold.
- Hardy-Weinberg equilibrium
-
1. All individuals have equal rates of survival success. Natural Selection does not occur.
2. No mutations (affecting the genes of individuals) occur which convert one allele to another.
3. No migration of individuals (gene flow) into or out of the population happens.
4. The population is sufficiently large (infinite) that no random events cause some individuals to pass on more of their genes than other individuals. Genetic drift does not occur.
5. All members of the population breed.
6. All individuals choose mates at random, i.e. "panmictic" mating is universal.
7. All individuals have equal rates of reproductive success. Sexual Selection does not occur.
Only if all of the above conditions are satisfied, then the relative frequencies of alleles and genotypes will not shift from generation to generation. Evolution will not take place. If any one of the above seven constraints is violated, then alleles shift and evolution occurs. In nature, such an equilibrium does not exist. (Condition 4 above - trivially - does not hold)
The observable violation of Hardy-Weinberg equilibrium in natural populations set the scene for population genetics (the techniques of Fisher, Haldane and Wright) to emerge and dominate evolutionary biology, during the early Modern Synthesis. Evolution was unpacked through mathematical analyses of allele and genotype frequencies.
The Hardy-Weinberg model - on its most superficial level of interpretation - points-out that evolution is a fundamental feature on the part of organisms (and in populations). Only if - in a population, there's no Natural Selection, no mutations, no migration of organisms into (or out of) it, no unpredictable events such as floods, hurricanes, earthquakes, climate change, etc., no finite population size and no Sexual Selection occurring - then allele and genotype frequencies within that population will remain in a state of equilibrium.
equations
By two, simple algebraic equations, calculations from them allow us to determine whether evolution has taken place in a given population.
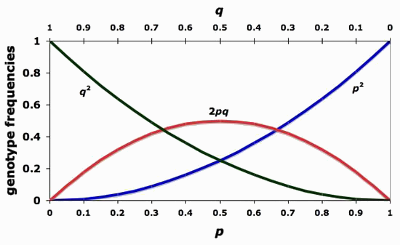
p^2 + 2pq + q^2 = 1
p + q = 1
p
frequency of the dominant allele in the population
q
frequency of the recessive allele in the population
p^2
percentage of homozygous dominant (XX) individuals
q^2
percentage of homozygous recessive (xx) individuals
2pq
percentage of heterozygous (Xx) individuals
- An example problem
- Assume that a population is in Hardy-Weinberg equilibrium. (If the population were not in equilibrium, then the following calculations would be in error.)
Suppose that there are 16 pigs in a poke, 12 pigs have pink coats and 4 pigs have black coats.
(1) Calculate for the percent of the population that are homozygous recessive, or q^2.
Since four of the sixteen individuals show the recessive phenotype (the black coat), the answer is 25% or 0.25.
(2) Find the frequency of the recessive allele, or q.
Since the square root of q^2 yields q (the frequency of the recessive allele), the answer is 0.5.
(3) Find the frequency of the dominant allele, or p.
Since the sum of the frequencies of both alleles = 100%, p + q = 1 and q = 0.5, the answer is (p = 1 - 0.5) = p = 0.5.
(4) Find the frequency of the heterozygotes, or 2pq.
Since the frequency of the heterozygotes is 2pq (the percent of the population that is heterozygous for the pink coat), the answer is 2pq = 2(0.5) (0.5) = 0.5. Or, 50% of the population is heterozygous.
(5) Since 25% of the population is homozygous recessive and 50% of the population is heterozygous, what percentage is homozygous dominant?
100% - 25% - 50% = 25%